Lost qKeys -- Pwn2Win 2020
Lost qKeys – Pwn2Win 2020
Points: 314 (dynamic, 16 solves)
Given:
nc quantum.pwn2.win 1337; lost_qkeys_48a8dcf3c4a7394a33d62abe94a13cd5e64a21029d17a373e2a3a221a66590dc.tar.gz
tldr
-
The service asks to input a
passwdthat is sent and encoded by theLocalQuantumComuputerand decoded byRemoteQuantumComputer. This is pretty much useless for the challenge. -
The returned bitstring is the measurement output (computational basis) of the
flagencoded in qubits, with a Hadamard gate applied with 50% prob. (bit ofkey, from/dev/urandom), and a Hadamard gate (bit ofpasswd, user controlled, just make it 0). -
There is a bias in the measurement towards the flag bit, as if the flag bit is 0, the probability to get the output 0 is 75%, same for bit 1. This is more than enough to recover the flag.
attack
The server file uses qiskit, a quantum computing framework, to implement a two-way communication between a LocalQuantumComputer (us) and a RemoteQuantumComputer (the server). There are many introductory texts on quantum computing, and they should be enough to understand the solution to this challenge, I won’t make another tutorial on this writeup.
The execution starts with our LocalQuantumComputer making a classical password into qubits |0> and |1>, represented by *P* below. Each bit is encoded using the Shor code error correction. Then, they are sent to the RemoteQuantumComputer server using a noisy quantum channel, which then decodes the bits. The circuit is (local encoding --- remote decoding):
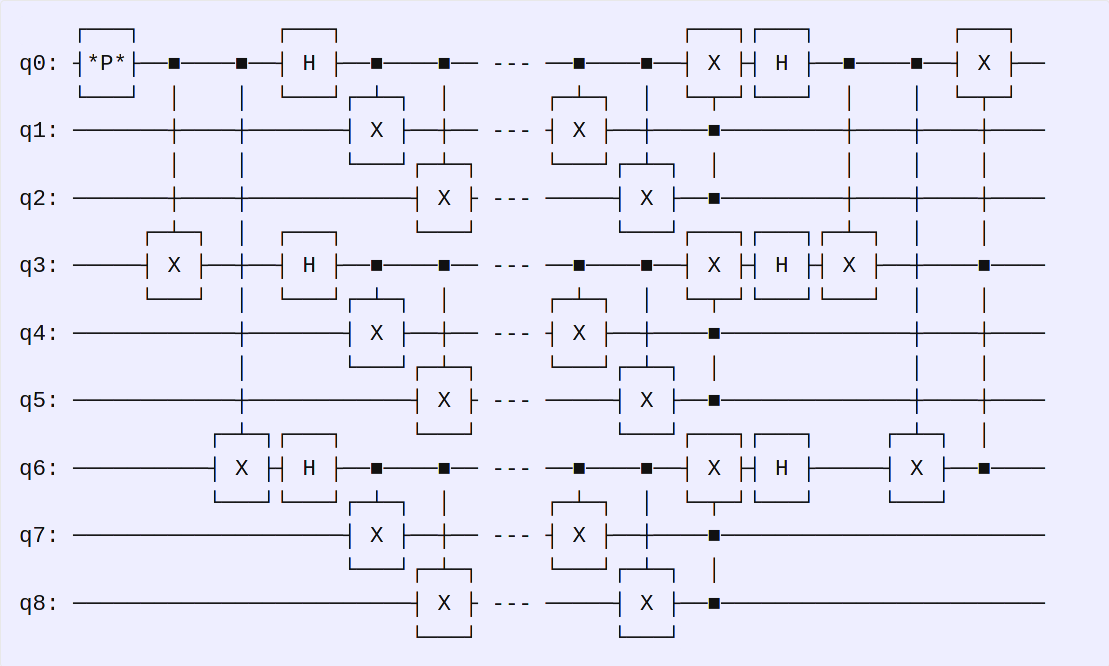
After, the RemoteQuantumComputer server takes a new qubit register qF with the flag bit encoded in a qubit *F* (|0> or |1>), takes a bit string from /dev/urandom and applies the Hadamard gate *K* if the random bit is 1. It takes the passwd, now in register q0, and applies an Hadamard gate to qF if the bit was 1. Then, it performs a measurement and the result goes to the classical register c0. The full circuit is (for 1 bit of the flag):
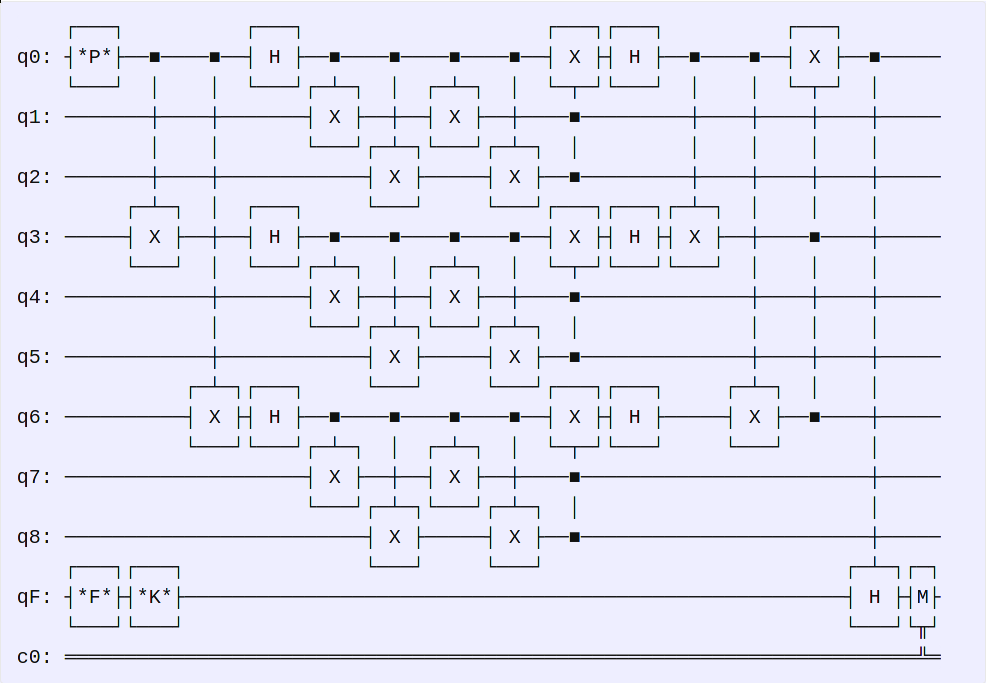
So, the first thing in the solution is that we control the passwd. Let’s set the passwd *P* to 0, meaning there is no Hadamard gate being applied to qF right before measuring. Everything is done bit-by-bit, therefore, the flag register qF is only the encoded flag bit *F*, with a Hadamard gate *K* applied only if a bit from /dev/urandom is 1. Finally, a measurement in the computational basis is performed on the registry qF into registry c0. There are four options:
Flag bit *F* |
Key bit *K* |
Outcome probabilities |
|---|---|---|
| 0, |0> | 0, Identity | 0 (100%) |
| 0, |0> | 1, Hadamard | 0 (50%), 1 (50%) |
| 1, |1> | 0, Identity | 1 (100%) |
| 1, |1> | 1, Hadamard | 0 (50%), 1 (50%) |
See, if the flag bit is 0, there is 75% probability of the outcome to be 0. And, if the flag bit is 1, there is 75% probability of the outcome to be 1. By repeating the experiment a few times (say 50), one can extract each bit and recover the entire flag.
CTF-BR{_1s_th4t_HoW_u_1mPl3meNt_@_QUantUm_0ne_t1m3_paD_???}
resources:
The solution code can be found in stt_lostqkeys.py.
