Horst

by goulov and mandlebro

Points: 200 (41 solves)

Description:

They say 3 rounds is provably secure, right?

Given: horst.py data.txt

Solution:

TLDR

With SymPy, compute the symbolic expressions of Encrypt and Decrypt in the (non-commutative) permutation group (or do it by hand, depending on your patience level).
Use properties of permutations to manipulate the expressions and obtain a pair \((\overline x, x)\), where \(\overline x\) is the conjugate permutation of \(x\) with the key.
Considering the property that conjugate permutations have the same cycle type, recover the key by trying all possibilities for each cycle, and using the second plaintext-ciphertext pair for testing.

Description

We are given two plaintext-ciphertext pairs. Each plaintext (\(p\)) and ciphertext (\(c\)) consists of a tuple of two permutations. The key \(k\) is just a single permutation.

The description of the challenge makes reference to the fact that a 3-round Feistel cipher is proved to be a pseudorandom permutation if the round function is a cryptographically secure pseudorandom function (Luby-Rackoff). In our case, the round key is always the same (\(k\)), the operation (\(\oplus\)) is composition of permutations (\(\circ\)), and the round function (\(F\)) is the permutation conjugation.

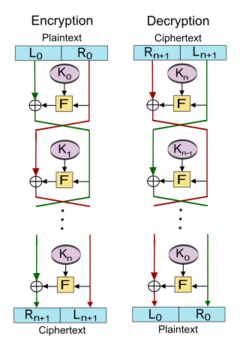
Everything here works in a permutation group, where the group operation (composition of permutations) is non-commutative. This makes the manipulation and symbolic computation of the system quite difficult. However, SymPy, namely sympy.symbols('x', commutative = False), allowed a much easier manipulation for the equations (although it couldn’t compute the solution for the system).

The cryptosystem has two parameters:

\(M = 3\) – number of rounds
\(N = 64\) – dimension of the permutations

The algorithms to encrypt is given by: \begin{align} Enc(k,p) = (&p_2 \circ k^{-1} \circ p_1 \circ k^{-1} \circ p_2 \circ k \circ k, \\ & p_1 \circ k^{-1}\circ p_2\circ p_2 \circ k^{-1}\circ p_1\circ k^{-1}\circ p_2\circ k \circ k\circ k), \end{align} where the plaintext and the ciphertext \((p = (p_1,p_2), c = (c_1,c_2))\) are both tuples of permutations. Essentially, we will focus on the encryption function \(Enc\).

Interestingly, we are also given a function to compute the decomposition of a permutation in the product of its disjoint cycles. Maybe there is something useful there besides notation…

Permutations

A set of permutations on a given set (\(\{0,\dots,63\}\), in our case) with the operation of composition of permutations from a group. An important property of this group is that its operation is in general non-commutative. You can read more about permutation groups in Wikipedia.

Permutations can be written in cyclic notation, \(\sigma = \alpha_1\alpha_2\cdots\alpha_n\) where \(\alpha_i\) are the cycles. One interesting thing to note is that disjoint cycles commute. This small point brought some problems in the final part when implementing the solution (we’ll discuss this later).

Cycle type

The cycle type of a permutation is defined as the lenghts of the cycles of a permutation, when written in its unique disjoint cycle decomposition. Two permutations have the same cycle type, if they have the same number of cycles of equal length.

The concept of cycle type will be crucial in solving the challenge. Particularly, the fact that conjugate permutations have the same cycle type.

Conjugate permutation

The conjugate permutation of a permutation \(\sigma\) will be shortened as \(\overline{\sigma}\). Conjugating a permutation \(\sigma\) by another permutation \(\tau\) (in the same permutation group) is given by \(\overline{\sigma} = \tau\sigma\tau^{-1}\). In the given cryptosystem, conjugation is always relative to the key-permutation \(k\) (i.e. \(\tau = k\)).

Encryption consists of three rounds, starting with the plaintext \((x^{(0)}=p_1,y^{(0)}=p_2)\). Upon close inspection, one may see that at each round \((x^{(i+1)}=y^{(i)},\quad y^{(i+1)}=x^{(i)}\circ \overline{y^{(i)}})\). So, while \(x^{(i+1)}\) becomes \(y^{(i)}\), \(y^{(i+1)}\) is computed as the composition of \(x^{(i)}\) with the conjugate of \(y^{(i)}\).

One important property to note is that the composition of conjugates equals the conjugate of the composition, \[\overline{\sigma}\circ\overline{\rho} = \overline{\sigma\circ\rho} \Leftrightarrow \left(\tau\circ\sigma\circ\tau^{-1}\right)\circ\left(\tau\circ\rho\circ\tau^{-1}\right) = \tau\circ\left(\sigma\circ\rho\right)\circ\tau^{-1}.\]

Therefore, the encryption may be described as \begin{align} Enc(k,(p_1,p_2)) &= (p_2 \circ \overline{p_1 \circ \overline{p_2}}, \quad p_1\circ\overline{p_2}\circ\overline{p_2\circ\overline{p_1\circ\overline{p_2}}}) \\[1em] &= (p_2 \circ \overline{p_1 \circ \overline{p_2}}, \quad p_1\circ\overline{p_2\circ\overline{p_2\circ\overline{p_1\circ\overline{p_2}}}}).\end{align}

Finally, the last thing required is understanding the workings of the cycle decomposition of the conjugate permutation. In fact, the cycle decomposition of the conjugate of \(\sigma\) can be obtained by permuting each cycle of the permutation \(\sigma\) according to the permutation \(\tau\). I.e. \[\overline{\sigma} = \tau(\alpha_1,\dots,\alpha_n)\tau^{-1} = \tau(\alpha_1),\dots,\tau(\alpha_k).\]

The attack

We figured out we had solved this challenge when noticed that \(p_1^{-1}\circ c_2\) is exactly the conjugate of \(p_2\circ c_1\), i.e., \[\overline{p_2 \circ c_1} = p_1^{-1} \circ c_2,\] where \((c_1,c_2)=Enc(k,p)\).

We had indeed found a pair \((\overline \sigma, \sigma)= (p_1^{-1}\circ c_2, p_2\circ c_1)\)! From here it will be possible to recover the permutation \(k\) using the last fact from the last section. Now let’s put everything together!

First, we know that both the permutation and its conjugate must have the same cycle type. We can easily compute and verify this is, in fact, true.

Next, given the cyclic description of both \(p_2 \circ c_1\) and \(p_1^{-1} \circ c_2\), we can use the cycle decomposition of the conjugate permutation to obtain the permutation by which the conjugation is made (i.e. \(\tau\), or concretely, \(k\)). However, this is slightly more complicated than it looks, since the cycles are (well…) cycles, we don’t know the correspondence of the labels. Handily, trying all possibilities just takes linear complexity in the product of the lengths of the cycles of the permutation (just try and rotate, for all cycles), and conveniently we have another plaintext-ciphertext pair to check if we found the correct \(k\).

The final issue (already mentioned) took some thinking. The problem was that the permutations had cycles with the same length, yielding two equal terms in the cycle type (this happened for both given pairs of plaintext-ciphertext). Combining the fact that disjoint cycles commute, we had also to try all the combinations while swapping these two cycles of same length. Once we found the issue, we could run our attack with success!

As described in the challenge, the FLAG was the SHA1 of the (permutation) key \(k\):

PCTF{69f4153d282560cdaab05e14c9f1b7e0a5cc74d1}

Resources:

The solution code can be found in sol.py.