Clutch - Hack The Box University CTF 2024

Given

The last objective is clear: steal the legendary artifact called "The Starry Spurr". Traveling to The Frontier Cluster, our space cowboys face a novel secure transmission system based on the nature of quantum physics. The team intercepts the public information exchanged between members of The Frontier Board. We are running out of time, the entrance is waiting for our command.

Source

here

TL;DR

Challenge implements a QKD protocol
Bob’s key derivation can be replicated using public information as long as we can discover which bases he used for measuring
We can use Z3 to reverse the sifting strings computation and obtain the relevant bases used by Bob

The Protocol

The first thing we noticed was the comment in line 15 of server.py

# Python implementation of the Frame-based QKD protocol described here : https://www.mdpi.com/2073-8994/12/6/1053

The paper presents a integral method for Quantum Key Distribution (QKD). By comparing it with the source, we see that the challenge relies on the implementation of the sifting framed protocol (section 5.4). Let’s dive into it:

Alice prepares and sends to Bob a pair of non-orthogonal qubits over the quantum channel. She chooses a pair randomly between \((\ket{0}_X, \ket{0}_Z)\), \((\ket{0}_X, \ket{1}_Z)\), \((\ket{1}_X, \ket{0}_Z)\) and \((\ket{1}_X, \ket{1}_Z)\).


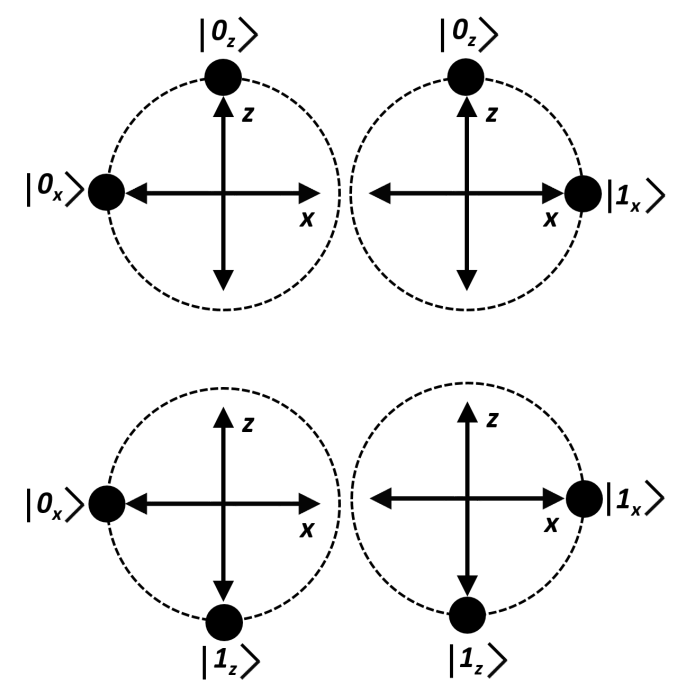non-orthogonal qubits

Bob chooses randomly the measurement basis (\(X\) or \(Z\)) to measure the incoming pair of non-orthogonal qubits.
After several rounds, using a classical channel, Bob announces to Alice the double matching detection events (rounds where Bob measures the same state on both qubits of the pair).
Alice computes the usable (\(f_i\) where \(i = 1 \dots 6\)) and auxiliary (\(i = 7 \dots 14\)) frames by iterative over pairs of double matching events. She shuffles that list of frames and sends it to Bob.


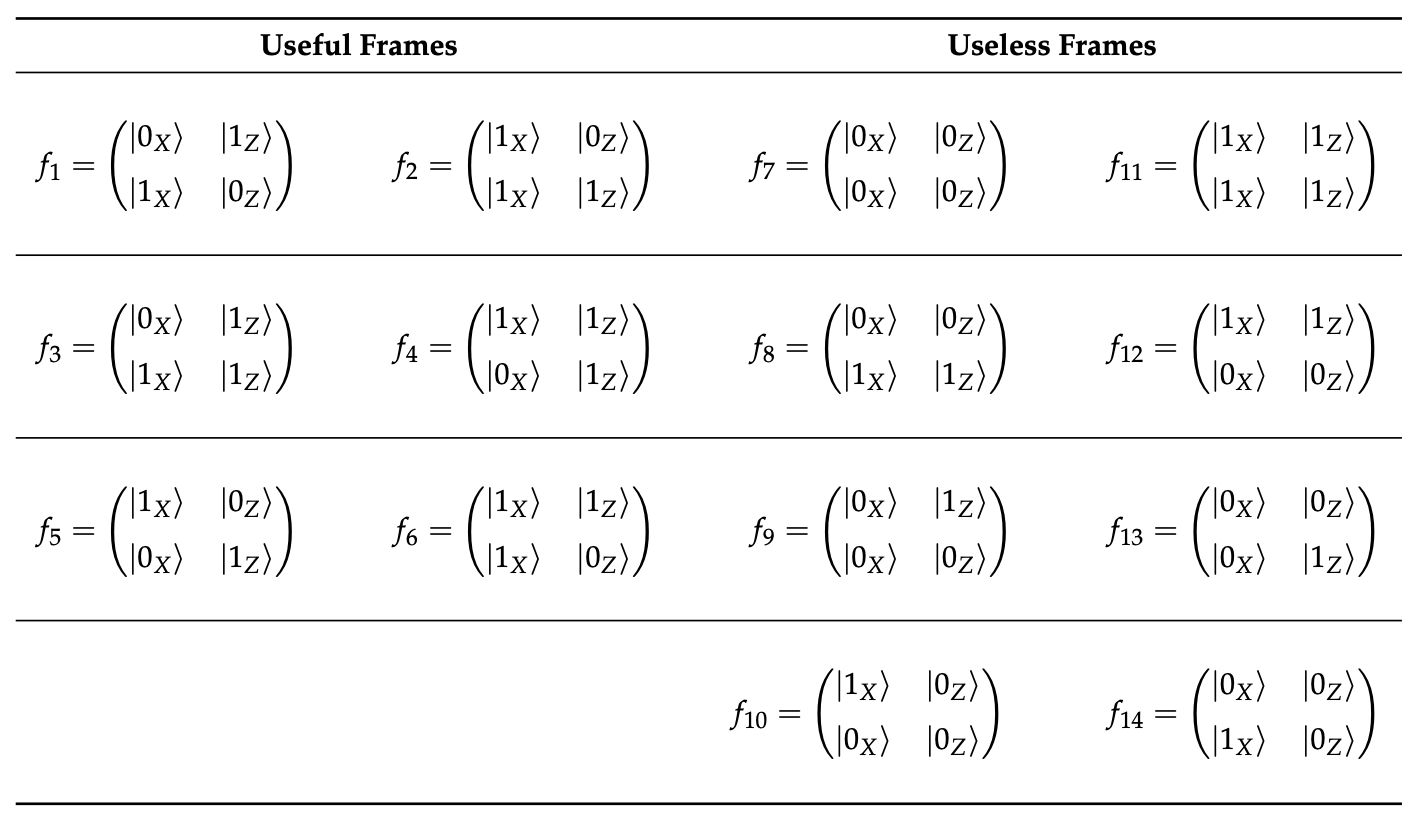frames

Bob computes the sifting bits of each frame and sends them back to Alice over a public channel.
Using the frames and corresponding sifting bits, Alice derives the secret bits.
On the other side, Bob computes the same secret bits.

Solution and Code Analysis

Some steps of the protocol don’t seem to exactly match the code, but we ended up solving the challenge without requiring deep knowledge about QKD.

Key Generation

alice_key = self.Alice.generate_shared_key(frames, usable_frames, ambiguous_frames, alice_sifting_strings, bob_sifting_strings)
bob_key = self.Bob.generate_shared_key(frames, ambiguous_frames,bob_sifting_strings)

if alice_key != bob_key:
    return {"error": "Key exchange failed, both keys are not equal. Retrying..."}

self.shared_key = alice_key.encode()

Our exploit uses a flaw in Bob’s key generation. Let’s focus on that part of the code:

Bob’s Key Generation

def generate_shared_key(self, frames, ambiguous_frames, sifting_strings):
    shared_secret = ""

    for frame in frames:
        if frame in ambiguous_frames:
            continue

        else:
            basis_orientation = (self.measurement_basis[frame[0]], self.measurement_basis[frame[1]])
            measurement_result = BOB_MR_DERIVATION[basis_orientation]
            shared_secret += KEY_DERIVATION[sifting_strings[frame]][measurement_result]

    return shared_secret

This function only depends on it’s arguments (frames, ambiguous_frames and sifting_strings), some hardcoded constants (BOB_MR_DERIVATION and KEY_DERIVATION, which are given to us in the helpers), and self.measurement_basis, which we will recover.

Analysing the use of Bob’s Measurement Basis

The measurement_basis seems to be chosen securely. According to line 91 of Bob’s source, we only need to recover the basis involved in non-ambiguous frames. Fortunately, those are exactly the ones that we can recover.

Notice that self.measurement_basis is only used in one other function:

def compute_sifting_bits(self, frame):
    sifting_bits = {
        "X": 0, 
        "Z": 0
    }
    
    for pair in frame:
        sifting_bits[self.measurement_basis[pair]] ^= int(self.measurement_results[pair][0])
        
    return ''.join(map(str, sifting_bits.values()))

This function is itself used as an auxiliary for compute_sifting_strings.

def compute_sifting_strings(self, frames):
    sifting_strings = {}

    for frame in frames:
        sifting_bits = self.compute_sifting_bits(frame)
        measured_bits = self.compute_measured_bits(frame)

        sifting_strings[frame] = f"{sifting_bits},{measured_bits}"

    return sifting_strings

On the other hand, compute_sifting_strings is only called once in server.py, in order to compute bob_sifting_strings. Note that only the output only includes the values of this dictionary.

Recovering Bob’s Sifting Strings

bob_sifting_strings = self.Bob.compute_sifting_strings(frames)

(...)

bob_sifting_strings = list(bob_sifting_strings.values())

        public = {
            "double_matchings": double_matchings,
            "frames": frames,
            "sifting_strings": bob_sifting_strings,
            "ambiguous_frames": ambiguous_frames
        }

Since Python preserves the key’s order, we can easily recover the whole dictionary bob_sifting_strings.

bob_sifting_strings = {}
for i, frame in enumerate(frames):
    bob_sifting_strings[frame] = sifting_bits[i]

Recovering Bob’s Measurement Basis

Using Z3, we can now recover self.measurement_basis for the qubits involved in the non-ambiguous frames.

We start by creating symbolic variables:

crafted_basis = {}

for i in range(256):
    crafted_basis[i] = BitVec('bob_{}_basis'.format(i), 1)

All we need now is to model the function compute_sifting_bits in Z3.

for i, frame in enumerate(frames):
    # Exploit compute_sifting_strings function from bob.py
    basis, mr = bob_sifting_strings[frame].split(',')
    basis = list(map(int, basis))
    mr = list(map(int, mr))
    i,j = frame

    x_s = BitVecVal(0,1)
    x_s = If(crafted_basis[i] == 1, x_s ^ BitVecVal(mr[0], x_s.size()), x_s)
    x_s = If(crafted_basis[j] == 1, x_s ^ BitVecVal(mr[1], x_s.size()), x_s)

    z_s = BitVecVal(0,1)
    z_s = If(crafted_basis[i] == 0, z_s ^ BitVecVal(mr[0], z_s.size()), z_s)
    z_s = If(crafted_basis[j] == 0, z_s ^ BitVecVal(mr[1], z_s.size()), z_s)

    s.add(x_s == basis[0])
    s.add(z_s == basis[1])

Last Steps

Great! Now we have Bob’s relevant measurement basis.

Remember that, in order to reproduce the key generation, we also need to recover generate_shared_key’s arguments: (frames, ambiguous_frames, bob_sifting_strings).

frames: this is given to us as part of the output.
ambiguous_frames: this is also part of the output.
bob_sifting_strings: we showed how to recover the keys above, the values are given as part of the output.

Therefore, now we have all we need to generate the shared key and get the flag!

Conclusion

The solution script can be found here.

$ python3 solve.py 
b'{"status": "OK", "QBER": 0.439468604086248}\n{"info": "Initialization completed. Only trusted ships can send valid commands"}\n> {"info": " Welcome to The Frontier Board, the coordinates of The Starry Spurr are (51.08745653315925, 1.1786658883433339). Today\'s secret code: HTB{n0w_7h475_4_C1u7Ch!_d3f1n3731Y_Fr4m3_b453d_QKD_n33d5_70_M47ur3__C0ngr47u14710n5!_e803174b4e75e48fedd8278473c83a02}"}\n'

Flag: HTB{n0w_7h475_4_C1u7Ch!_d3f1n3731Y_Fr4m3_b453d_QKD_n33d5_70_M47ur3__C0ngr47u14710n5!_e803174b4e75e48fedd8278473c83a02}