YAFM – Google CTF 2020

by goulov and ice

Points: 308 (18 solves)

Given: Yet Another Factorization Method. - nc yafm.2020.ctfcompetition.com 1337 - Attachment

tldr

A given RSA modulus is generated by multiplying two primes with very low Hamming weight
Factor it by iteratively finding solutions for \(pq = n \mod 2^k\) for an increasing \(k\)
For each \(k\), keep a fixed number of possible solutions - the ones with lower Hamming weight

Getting started

Connecting to the endpoint, we are given the chance to generate RSA keys and get the flag encrypted with those same keys. To parse the modulus we use the great pycryptodome:

from Crypto.PublicKey import RSA

with open('pubkey.pem','rb') as f:
....key = RSA.import_key(f.read())

n = key.n

Prime generation

The provided code tells us how the primes are generated: starting with \(1024\) bits with only the 2 MSBs and LSB set, sample 180 indices from \({1,\dots,1021}\) uniformly at random; set the corresponding bits to 0 or 1 also uniformly at random. The Hamming weight is then (on average) \(180/2 + 3 = 93\) for each of the \(1024\) bit primes.

def generate_prime(prime_len=1024):
....bits_len = 180
....while True:
........bits = random.getrandbits(bits_len)
........idxs = random.sample(list(range(1, prime_len-2)), bits_len)
........p = 1 | 2**(prime_len - 1) | 2**(prime_len - 2)
........for i in range(bits_len):
............p += (bits >> i & 1)*2**idxs[i]
........if isPrime(p):
............return p

Factoring the modulus

Given the modulus \(n = pq\), with \(p\) and \(q\) of this form, raised the following interesting question: How may one factor a composite number given that its factors have low Hamming weight? Answering this question will give us the flag.

Using BFS

The algorithm consists of inductively finding solutions to \(pq = n \mod 2^{k+1}\) given solutions to \(pq = n \mod 2^k\).

Base case

We’ll enumerate possible solutions using the following encoding: \((w_{sum}, p, q)\), where \(w_{sum}\) is the sum of the Hamming weight of each of the primes which we use to sort our list by total Hamming weight.

For \(k=1\) we know the list of solutions (sols) consists of

sols = [(2,1,1)]

Iterative search

Starting from the base, we will enumerate the possible solutions for higher values of \(k\), ordering them by the total Hamming weight of both the primes, and discarding a number of solutions above a fixed threshold.

for k in range(1, 1022):
....sols = find_sols_Kplusone(n, sols)

We start with an empty list, and to avoid adding repeated values (p,q) or (q,p) we also maintain a hash table with the pairs that we have already seen.

def find_sols_Kplusone(n, solsK):
....solsK = []
....seen = {}
....n_mod_k = n % 2**k

\((x,y) = (p,q)\) is a solution for \(xy = n \mod 2^{k+1}\) if and only if it is a solution for \(xy = n \mod 2^k\). So, to construct the \(k+1\) list of solutions, we iterate over our current solutions and for each pair (p,q) we consider four possible solutions for \(k+1\) like so:

....for weight, p,q in solsK:
........p2 = p + 2**k
........q2 = q + 2**k
........n1 = p*q % 2**k
........n2 = p2*q % 2**k
........n3 = p*q2 % 2**k
........n4 = p2*q2 % 2**k

Finally, we check if each of those four solutions is valid, and if so, we add them to our list of solutions in an ordered manner (i.e. prioritized by total Hamming weight). We only keep a fixed number of solutions, otherwise the number of solutions would grow exponentially at each step. But, the solution will still be in the list with high probability, since given the Hamming weight of the correct solution is very low, the solution will be in the beginning of our list of solutions.

........#analogously for n2,n3 and n4
........if n1 == n_mod_k and (p,q) not in seen:
............bisect.insort(solsk, ((weight, p,q)))
............seen[(p,q)] = True
............seen[(q,p)] = True

Example

example

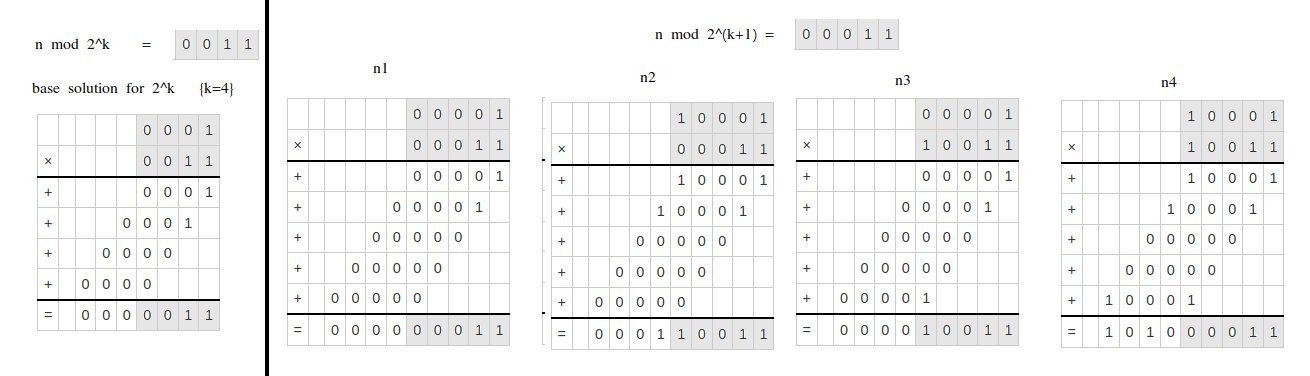
In this example we would add n1 and n4 to the list. n1 would be closer to the beginning of the list of solution because the hamming weight of its components (p,q) is lower than those of n2.

Convergence - How many solutions to keep?

Our algorithm is empirical, meaning that there is no guarantee that the solution will be found. Indeed, that would only be possible keeping the entire exponential tree of solutions. Still, we found that keeping 2000 solutions is enough to factor the majority of public keys generated in this manner, while having a reasonable computation time (~10s).

CTF{l0w_entr0py_1s_alw4ys_4_n1ghtmar3_I_h4v3_sp0ken}

The final solution script is provided here.

Applying the same strategy for other problems

Having answered the first question raised by this CTF challenge, we also wondered: Can this factoring technique be used in other similar problems for primes with different structures?

Indeed, this factorization technique can also be applied to other kinds of weaknesses in prime generation. We abstract this method by not directly concerning about low/high Hamming weight, but how to differentiate correct from incorrect solutions to the equation \(pq = n \mod 2^k\) for any \(k\). This CTF challenge is then one particular instance of that abstraction.

We give another instance that fits in our generalization: Suppose your PRNG had a perfect bit balance (generates the same number of ones and zeros). But, for each pair of generated bits, one was “truly random” and the other was the complement of the first. This would still be vulnerable to our technique, because one can still differentiate correct solutions for the aforementioned equation. We give an implementation of our technique to this new example here.

Wrap up

This challenge was solved by 18 teams, out of the 625 signed up for Google CTF 2020, it was the third least solved cryptography challenge. It asked the players to factor a composite number with ill-generated primes based on their low Hamming weight.

We did not only solve the challenge itself but also generalized our result to a broader set of weaknesses in prime generation, using the ability do distinguish the solutions for the equation \(pq = n \mod 2^k\), for any \(k\).

All in all, this was an excellent challenge. Next time we see an RSA modulus being generated with a bad PRNG we will think of this.