Quantum Pyramids – Google CTF 2020

by goulov and ice

Points: 373 (9 solves)

Given: A super efficient post-quantum signature scheme has been deployed. Can you forge a signature? - quantumpyramids.zip - https://quantumpyramids.web.ctfcompetition.com/

tldr (assuming you know SPHINCS+)

  1. We’re given an instance of SPHINCS+ with “efficient” (meaning small) parameters, a target message, an oracle that signs any (non-target) messages, and an endpoint that verifies a signature where a forgery of the target must be submitted.

  2. For the hypertree structure with WOTS+ signatures, these parameters make selecting an arbitrary leaf easy, yielding the required authentication data and allowing one to get many signatures for the same FORS instance.

  3. For the FORS signature, the parameters allow recovering the FORS secret key given enough signatures, and thus FORS-sign arbitrary messages. So, we now have everything we need to create the forged signature and get the flag.

tldr SPHINCS+ intro (assuming you know FORS & WOTS+)

  1. SPHINCS+ is a post-quantum signature scheme based on hash functions, running for the NIST PQC Standardization. It uses two types of hash-based signatures, FORS few-time signatures (FTS) and WOTS+ one-time signatures (OTS).

  2. The two are connected using a hypertree (HT) of Merkle trees, which is parametrized by the height \(h\) and number of layers \(d\). The secret key (\(sk\)) is a random seed, the public key (\(pk\)) is the root of the HT and a random seed.

    The HT leaves of each layer are WOTS+ public keys: in the intermediate layers they verify the signature of the root of the tree below; in the bottom layer they verify the signature of the FORS public keys. The FORS instance is fixed (out of \(2^{h/d}\)) for each signature and computable from public information, and a message \(m\) is signed using this instance.

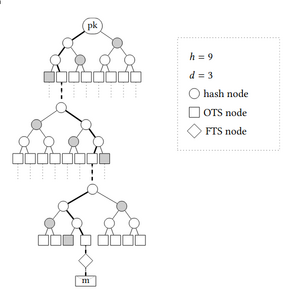
    SPHINCS+ structure (Fig.1 from https://sphincs.org/data/sphincs+-paper.pdf)

    SPHINCS+ HT, hash nodes as in a Merkle signature, with authentication path in gray

  3. Structure of a SPHINCS+ signature: \([\ R\ ||\ sig^{FORS}\ ||\ sig^{WOTS+}\ ]\), \(R\) is a random value computed from the secret key, message, and uniformly sampled randomness.

    \(sig^{FORS}\) (FORS signature of the message) and \(sig^{WOTS+}\) (WOTS+ signature of the HT) include both the signatures and the authentication paths as in a Merkle signature (hashes of the nodes needed to compute the root).

tldr how FORS and WOTS+ work in SPHINCS+

  1. A FORS (Forest Of Random Subsets) few-time signature scheme is parametrized by \((k, t = 2^a)\). The secret key is made of \(k\) lists of \(t\) elements each, and is derived from the SPHINCS+ keys. Each of the \(kt\) elements is a leaf of one of \(k\) Merkle trees, and the public key is the combined hash of the \(k\) roots \(r_i\).

    The FORS instance and message digest are computed as \((digest\ ||\ idx) = \mathsf{H}(R, pk, m)\). To sign, the digest is split into \(k\) \(a\)-bit integers, seen as a list of indices that select a secret key value from the corresponding list, concatenated with the authentication path. To verify, the roots are computed and hashed together, and compared with the public key.

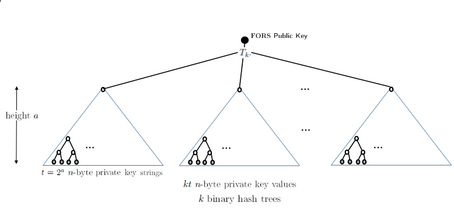
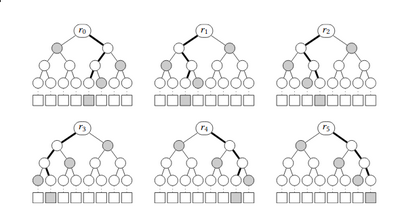
    FORS structure (Fig.10 from https://sphincs.org/data/sphincs+-round2-specification.pdf) FORS structure (Fig.3 from https://sphincs.org/data/sphincs+-paper.pdf)

    FORS structure for \((k=6, a=3)\), hash nodes as in a Merkle signatures, with authentication paths in gray.

  2. The WOTS+ one-time signature scheme is parametrized by \((n, w)\). The secret key is a series of \(\ell = n/\log(w)\) values derived from the SPHINCS+ secret key. The public key is the chained \(w\)-time hashing of each secret key value, and depend on the address in the HT and SPHINCS+ public key.

    A message is split into \(\ell\) distinct \(\log(w)\)-bit integers, and the signature amounts to hashing each element of the secret key this number of times, together with a checksum.

  3. The HT structure is computed by applying a hash function to each pair of nodes using the paths from the leaves to the root, for each subtree. As the leaves of the intermediate trees are deterministically generated WOTS+ public keys, the HT is never computed in full. This means that given the FORS instance, the \(sig^{WOTS+}\) part of the signature is fixed.

    Consequently, using the HT structure is more efficient than simply increasing the height of a tree, but it must be (very) large so the same leaf node is not selected many times.

tldr how to forge a signature

  1. The SPHINCS+ HT with the given parameters has 2 layers of height-2 Merkle trees, so there is a total of 16 possible FORS choices. Hence, with probability \(1/16\), a message will be signed with a certain FORS instance. But(!) we have access to as many signatures as we want, and FORS is a few-time signature scheme, so this can’t be good…

  2. The parameters for FORS set the number of trees \(k=17\) and the height of the trees \(a=6\) (\(t=2^a=64\)). Thus, FORS signs message digests of 17 6-bit characters, meaning that the secret key has \(kt = 17\cdot 64 = 1088\) elements.

    Each signature for the same FORS instance leaks 17 random elements of the FORS secret key and their authentication path. So, it is possible to keep requesting signatures for the same instance, until the full secret key is recovered. Now, for that instance, we can FORS-sign arbitrary messages, which we do for the target message.

  3. Although \(R\) is supposed to be computed from the secret key, this doesn’t matter: as \(R\) is sent in the signature, we may sample it at random, as the verifier doesn’t have the secret key to check its authenticity anyway…

    So, we just pick any \(R\) that, together with the message and public key, gives the path we want, and include it in the forged signature. Then, we take the WOTS+ signature from any provided signature that follows the same HT path. These, with the forged FORS signature on the target message, make the final forged SPHINCS+ signature.

the attack

Well… Surprise! Everything has been covered already, not too long after all! The only remaining thing to do is submit the forged signature to the endpoint and get the flag!

CTF{t00_m4ny_h4$h3s_f0r_t0d4y}

the end…

Quantum pyramids was the least solved cryptography challenge of Google CTF 2020. It was an interesting task on the subject of hash-based signatures, using the state-of-the-art scheme SPHINCS+. Unfamiliarity with the type of scheme, together with the fact that there is no simple implementation that I’m aware of (e.g. in python), led to A LOT of reading.

Therefore, I decided to try to simplify everything as much as I was able to in this write-up, with this funny top-down-looking design, based on the usual tldr section of a typical write-up. Hopefully you enjoyed reading it and learned a few things : )

resources:

The solution code can be found in sol.zip. Everything in this writeup is heavily based on https://sphincs.org/data/sphincs+-paper.pdf and https://sphincs.org/data/sphincs+-round2-specification.pdf.